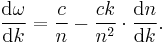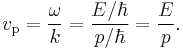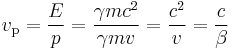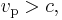Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and period T as
Or, equivalently, in terms of the wave's angular frequency ω, which is the number of oscillations per unit of time, and wavenumber k, which is the number of oscillations per unit of space, by
To understand where it comes from, imagine a basic sine wave, A cos (kx−ωt). Given time t, the source produces ωt oscillations. At the same time, the initial wave front propagates away from the source through the space to the distance x to fit the same amount of oscillations, kx = ωt. So that the propagation speed v is v = x/t = ω/k. The wave propagates faster when higher frequency oscillations are distributed less densely in space.[1] Formally, Φ = kx−ωt is the phase. Since ω = −dΦ/dt and k = +dΦ/dx, the wave speed is v = dx/dt = ω/k.
Contents |
Relation to group velocity, refractive index and transmission speed
Since pure sine wave cannot convey any information, some change in amplitude or frequency, known as modulation, is required. By combining two sines with slightly different frequencies and wavelengths,
the amplitude becomes a sinusoid with phase speed of vg = Δω/Δk. It is this modulation that represents the signal content. Since each amplitude envelope contains a group of internal waves, this speed is usually called the group velocity.[1] In reality, the vp = ω/k and vg = dω/dk ratios are determined by the media. The relation between phase speed, vp, and speed of light, c, is known as refractive index, n = c/vp = ck/ω. Taking the derivative of ω = ck/n, we get the group speed,
Noting that c/n = vp, this shows that group speed is equal to phase speed only when the refractive index is a constant: dn/dk = 0.[1] Otherwise, when the phase velocity varies with frequency, velocities differ and the medium is called dispersive. The phase velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed the speed of light in a vacuum, but this does not indicate any superluminal information or energy transfer. It was theoretically described by physicists such as Arnold Sommerfeld and Léon Brillouin. See dispersion for a full discussion of wave velocities.
Matter wave phase
In quantum mechanics, particles also behave as waves with complex phases. By the de Broglie hypothesis, we see that
Using relativistic relations for energy and momentum, we have
where E is the total energy of the particle (i.e. rest energy plus kinetic energy in kinematic sense), p the momentum,  the Lorentz factor, c the speed of light, and β the speed as a fraction of c. The variable v can either be taken to be the speed of the particle or the group velocity of the corresponding matter wave. Since the particle speed
the Lorentz factor, c the speed of light, and β the speed as a fraction of c. The variable v can either be taken to be the speed of the particle or the group velocity of the corresponding matter wave. Since the particle speed 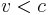 for any particle that has mass (according to special relativity), the phase velocity of matter waves always exceeds c, i.e.
for any particle that has mass (according to special relativity), the phase velocity of matter waves always exceeds c, i.e.
and as we can see, it approaches c when the particle speed is in the relativistic range. The superluminal phase velocity does not violate special relativity, as it carries no information. See the article on signal velocity for details.
Slow phase velocity and superluminality
Contrarily, a subluminal phase velocity may be corresponding to a velocity faster than light, i.e. 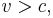 because the product is constant
because the product is constant 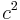 .[2][3] For example, the phase velocity of commercial electric power (frequency 60Hz) in copper is 3 m/s according to the original definition
.[2][3] For example, the phase velocity of commercial electric power (frequency 60Hz) in copper is 3 m/s according to the original definition 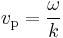 . Thus, the velocity
. Thus, the velocity  should be 108 c on account of
should be 108 c on account of 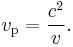 The value equals energy flow velocity
The value equals energy flow velocity 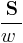 of the field given by classical electrodynamics (
of the field given by classical electrodynamics ( is Poynting vector and
is Poynting vector and  is energy density).
is energy density).
See also
- Wave propagation
- Group velocity
- Propagation delay
- Wave propagation speed
- Dispersion (optics)
- Shear wave splitting
References
- ^ a b c "Phase, Group, and Signal Velocity". Mathpages.com. http://www.mathpages.com/home/kmath210/kmath210.htm. Retrieved 2011-07-24.
- ^ Wang, Zhong-Yue (2011). "Superluminal energy transmission in the Goos-Hanchen shift of total reflection". Optics Communications 284 (7): 1747–1751. Bibcode 2011OptCo.284.1747W. doi:10.1016/j.optcom.2010.12.027.
- ^ Zhong-Yue Wang. Energy transport faster than light in good conductors. arXiv:/1101.1840.
- Brillouin, Léon "Wave Propagation And Group Velocity" Academic Press Inc., New York and London (1960) ISBN 0-12-134968-3.
- Main, Iain G. (1988).Vibrations and Waves in Physics. 2nd ed. New York; Cambridge University Press. ISBN 0-521-27846-5. 214-6 pp.
- Tipler, Paul A. and Ralph A. Llewellyn (2003). Modern Physics. 4th ed. New York; W. H. Freeman and Company. ISBN 0-7167-4345-0. 222-3 pp.
External links
- Subluminal, a Java applet
- Simulation, a Java applet by Paul Falstad
- Group and Phase Velocity - Java applet showing the difference between group and phase velocity.
| Velocities of waves |
|---|
| Phase velocity • Group velocity • Front velocity • Signal velocity |
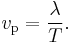
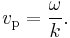
![\cos[(k-\Delta k)x-(\omega-\Delta\omega)t]\; %2B\; \cos[(k%2B\Delta k)x-(\omega%2B\Delta\omega)t] = 2\; \cos(\Delta kx-\Delta\omega t)\; \cos(kx-\omega t),](/2012-wikipedia_en_all_nopic_01_2012/I/7c8f8acc153055c4ceadd0f49f29f8f1.png)